一、定义 What is Machine Learning

二、建模 Model Representation

三、一元线性回归 Linear Regression with One Variable

3.1 一元线性归回的符号约定 Notation

3.2 一元线性回归 Linear Regression with One Variable

3.3 代价函数 Cost Function

3.4 梯度下降概述 Gradient Descent Outline

3.5 梯度下降算法 Gradient Descent Alg

3.5.1 同步更新参数 Simultaneously Update

3.5.2 收敛 Convergence

3.5.3 学习率的取值 evaluate alpha

3.5.4 梯度下降更新参数公式

四、多元线性回归 Multiple Features and Gradient Descent

4.1 多元线性归回的符号约定 Notation

4.2 多元线性回归 Linear Regression with Multiple Variables

4.3 估值、代价函数、梯度下降

4.4 多元线性回归的矩阵描述

4.5 平均值归一化 Mean Normalization

4.6 多项式拟合 Polynomial Regression

4.7 过拟合Overfit与欠拟合Underfit

4.8 一般等式、梯度下降和一般等式的比较

复习Andrew Ng的课程Machine Learning，总结线性回归、梯度下降笔记一篇，涵盖课程week1、week2。

一、定义 What is Machine Learning

有两种业界比较认可的对机器学习的定义。

一种是Aithur Samuel在1959年给出的定义。机器学习：不需要明确编程就能使计算机具有学习能力的研究领域。

另一种是Tom Mitchell在1998年给出的定义。适定学习问题：如果一个计算机程序在任务T上的性能(以P衡量性能)随着经验E的提高而提高，那么它就被称为从经验E对某些任务T和性能度量P的学习。（拉倒吧，还是看英文原文吧！）

Machine Learning Definition
-Aithur Samuel 1959. Machine Learning: Field of study that gives computer the ability to learn without being explicitly programmed.
-Tom Mitchell 1998. Well-posed Learning Problem: A computer program is said to learn from experience E with respect to some task T and performance measure P, if its performance on T, as measured by P, improves with experience E.

二、建模 Model Representation

机器学习分很多种类

Supervised Learning 有监督的学习
Unsupervised Learning 无监督的学习
Reinforcement learning 强化学习
Recommender System 推荐系统

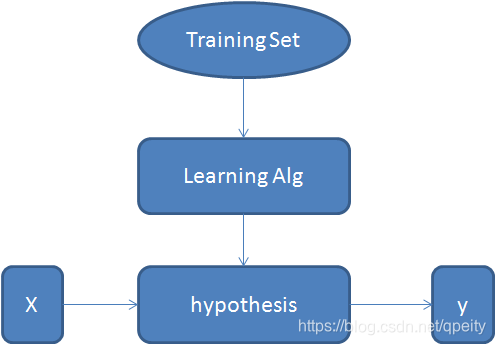
但是他们的建模几乎是一样的。都是通过在训练集（Training Set）上运行学习算法（Learning Alg）得到估值函数（hypothesis），这个假设函数可以对输入的特征X进行预测（估计 estimated value），输出y。

三、一元线性回归 Linear Regression with One Variable

3.1 一元线性归回的符号约定 Notation

约定一元线性回归问题中的符号定义。

$m=Number\ of\ training\ examples$ 训练集的大小。

$x's=input\ variable/feature$ 输入变量，也就是特征。

$y's=output\ variable / target\ variable$ 输出变量，也就是估值。

$(x,y)=one\ training\ example$ 一个训练用例。

$(x^{(i)},y^{(i)})= the\ i^{th}\ training\ example$ 训练集中的第i个用例。

3.2 一元线性回归 Linear Regression with One Variable

一元线性回归，Linear Regression with One Variable也叫做Univariate Linear Regression。其输入特征是一维的，输出值也是一维的。估值为 $h_{\theta }(x)=\theta _{0}+\theta _{1}x$ 。一元线性回归的思想是，选择合适的 $\theta _{0}$ 和 $\theta _{1}$ 使 $h_{\theta }(x)$ 对训练集 $(x,y)$ 上的 $x,\ h_{\theta (x)}$ 接近 $y$ 。

Idea: Choose $\theta _{0}$ $\theta _{1}$ so that $h_{\theta }(x)$ is close to $y$ for our training example $(x,y)$ .

minimize $\sum_{i=1}^{m} (h_{\theta }(x^{(i)})-y^{(i)})^{2}$

3.3 代价函数 Cost Function

Cost Function Definition is square error function. 代价函数是平方误差函数。这个函数用来衡量估值与真实值之间的偏差。

代价函数是

$J(\theta _{0},\theta _{1})=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})^{2}$

其中 $h_{\theta }(x)=\theta _{0}+\theta _{1}x$ 。使 $J(\theta _{0},\theta _{1})$ 最小的 $\theta _{0}$ 和 $\theta _{1}$ 值确定 $h_{\theta }(x)$ 。公式里面为了表示“平均”，所以除以 $m$ ，但为什么不简单的就写个 $m$ 而是 $2m$ 呢？因为后面求导数的时候，平方的求导会把这个2抵消掉，这样导数式的样子就和逻辑回归问题的导数式子形式上统一了。

注意：

$J(\theta _{0},\theta _{1})$ 是关于 $\theta _{0}$ $\theta _{1}$ 的函数， $x^{(i)}$ 和 $y^{(i)}$ 是参数。也就是说求取导数的时候，变量是 $\theta _{0}$ $\theta _{1}$ 。
$h_{\theta }(x)$ 是关于 $x$ 的函数， $\theta _{0}$ $\theta _{1}$ 是参数。

3.4 梯度下降概述 Gradient Descent Outline

Have some function $J(\theta _{0},\theta _{1})$ , Want $\min_{\theta_{0},\theta _{1}}{J(\theta_{0},\theta _{1})}$

Outline：

Start with some $\theta _{0}$ $\theta _{1}$
Keep changing $\theta _{0}$ $\theta _{1}$ to reduce $J(\theta _{0},\theta _{1})$ until we hopefully end up at a minimum.

梯度下降的思想就是，我们先假定有 $\theta _{0}$ $\theta _{1}$ 有某个值，通过改变 $\theta _{0}$ $\theta _{1}$ 的值使 $J(\theta _{0},\theta _{1})$ 减小，直至得到最小值。

3.5 梯度下降算法 Gradient Descent Alg

3.5.1 同步更新参数 Simultaneously Update 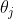$\theta _{j}$

重复进行

$\theta _{j}\ $:=$\ \theta _{j}-\alpha \cdot\frac{\partial J(\theta _{0},\theta _{1})}{\partial \theta _{j}}$ ，

其中 $\alpha$ 是学习率（learning rate），必大于0。

注意，这种更新是各个维度上的同步更新，也就是说更新过程是这样的

$temp_{0} $:=$\ \theta _{0}-\alpha \cdot\frac{\partial J(\theta _{0},\theta _{1})}{\partial \theta _{0}}$

$temp_{1} $:=$\ \theta _{1}-\alpha \cdot\frac{\partial J(\theta _{0},\theta _{1})}{\partial \theta _{1}}$

$\theta _{0} $:=$\ temp_{0}$

$\theta _{1} $:=$\ temp_{1}$

3.5.2 收敛 Convergence

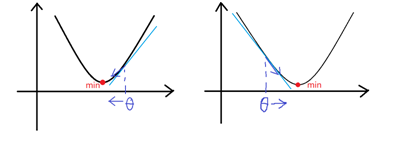
对于一元线性回归，代价函数 $J(\theta _{0},\theta _{1})$ 的几何形状是个碗状曲面，因此代价函数一定收敛。根据上面同步更新的公式，我们分两种情况讨论，示意图如下。

当 $\frac{\partial J(\theta _{0},\theta _{1})}{\partial \theta _{1}}> 0$ 时， $\theta$ 减小，趋向于收敛；

当 $\frac{\partial J(\theta _{0},\theta _{1})}{\partial \theta _{1}}< 0$ 时， $\theta$ 增大，也趋向于收敛；

3.5.3 学习率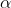 $\alpha$ 的取值 evaluate alpha

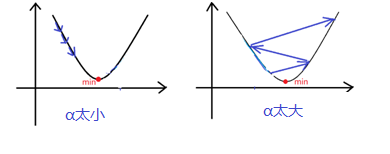
这个过程要注意学习率 $\alpha$ 的取值应适中。如果 $\alpha$ 太小，收敛速率低，学习缓慢。如果 $\alpha$ 太大，可能跳过minimum不能收敛，甚至发散。示意图如下。

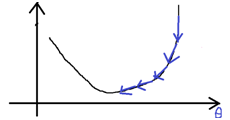
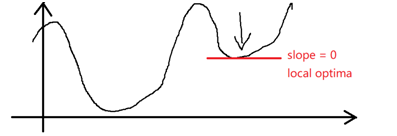
根据同步更新参数公式， $\theta _{j}\ $:=$\ \theta _{j}-\alpha \cdot\frac{\partial J(\theta _{0},\theta _{1})}{\partial \theta _{j}}$ ，随着接近minimum， $\frac{\partial J(\theta _{0},\theta _{1})}{\partial \theta _{j}}$ 逐渐减小。在接近minimum时，梯度下降自动减小步长，因此收敛的过程中不需要改变学习率 $\alpha$ 。示意图如下。

$\theta _{j}$ at local optima。经过学习获得的是局部最优解。

3.5.4 梯度下降更新参数公式

$J(\theta _{0},\theta _{1})=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})^{2}=\frac{1}{2m}\sum_{i=1}^{m}(\theta _{0}+\theta _{1}x^{(i)}-y^{(i)})^{2}$

由代价函数得到两个参数的偏导数函数。

当 $j=0$ 时， $\frac{\partial J(\theta _{0},\theta _{1})}{\partial \theta _{0}}=\frac{1}{m}\sum_{i=1}^{m}(\theta _{0}+\theta _{1}x^{(i)}-y^{(i)})=\frac{1}{m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})$ 。

当 $j=1$ 时， $\frac{\partial J(\theta _{0},\theta _{1})}{\partial \theta _{1}}=\frac{1}{m}\sum_{i=1}^{m}(\theta _{0}+\theta _{1}x^{(i)}-y^{(i)})x^{(i)}=\frac{1}{m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})x^{(i)}$ 。

四、多元线性回归 Multiple Features and Gradient Descent

4.1 多元线性归回的符号约定 Notation

约定多元线性回归问题中的符号定义。

$m=Number\ of\ training\ examples$ 训练集的大小。

$n=number\ of\ features$ 特征的维度大小。

$x^{(i)}=input\ (features)\ of\ i^{th}\ training\ example$ 第i个训练用例。

$x_{j}^{(i)}=value\ of\ feature\ j\ in\ i^{th}\ training\ example$ 第i个训练用例的第j维特征值。

4.2 多元线性回归 Linear Regression with Multiple Variables

多元线性回归的估值为 $h_{\theta }(x)=\theta _{0}+\theta _{1}x_{1}+\theta _{2}x_{2}+\theta _{3}x_{3}+\cdots+\theta _{n}x_{n}$

4.3 估值、代价函数、梯度下降

为了方便起见，我们给特征值增加一个维度，也就是 $x_{0}\equiv 1$ 。

特征值和参数都写作向量的形式：

$x=\begin{bmatrix} x_{0} \\ x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{bmatrix}\in \mathbb{R}^{n+1}$ $\theta =\begin{bmatrix} \theta_{0} \\ \theta_{1} \\ \theta_{2} \\ \vdots \\ \theta_{n} \end{bmatrix}\in \mathbb{R}^{n+1}$

估值写作矩阵相乘的形式：

$h_{\theta}(x)=x^{T}\theta=\theta _{0}x_{0}+\theta _{1}x_{1}+\theta _{2}x_{2}+\theta _{3}x_{3}+\cdots+\theta _{n}x_{n}$

代价函数：

$J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})^{2}$

同步更新参数，以使代价函数最小，对于每一个参数 $\theta_{j}$ 而言

$\theta _{j}$:=$\theta _{j}-\alpha \cdot \frac{\partial J(\theta)}{\partial \theta _{j}}=\theta _{j}-\alpha \cdot \frac{1}{m}\cdot \sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})x_{j}^{(i)}$

也就是说

$\theta _{0}$:=$\theta _{0}-\alpha \cdot \frac{1}{m}\cdot \sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})x_{0}^{(i)} \qquad ,\qquad x_{0}^{(i)}\equiv 1$

$\theta _{1}$:=$\theta _{1}-\alpha \cdot \frac{1}{m}\cdot \sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})x_{1}^{(i)}$

$\theta _{2}$:=$\theta _{2}-\alpha \cdot \frac{1}{m}\cdot \sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})x_{2}^{(i)}$

……………………

$\theta _{n}$:=$\theta _{n}-\alpha \cdot \frac{1}{m}\cdot \sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})x_{n}^{(i)}$

写作矩阵式

$\begin{bmatrix} \theta _{0}\\ \theta _{1} \\ \theta _{2} \\ \vdots \\ \theta _{n} \end{bmatrix}$:=$\begin{bmatrix} \theta _{0}\\ \theta _{1} \\ \theta _{2} \\ \vdots\\ \theta _{n} \end{bmatrix}-\alpha \cdot \frac{1}{m}\cdot \begin{bmatrix} x_{0}^{(1)} &x_{0}^{(2)} &x_{0}^{(3)} &\cdots &x_{0}^{(m)} \\ x_{1}^{(1)} &x_{1}^{(2)} &x_{1}^{(3)} &\cdots &x_{1}^{(m)} \\ x_{2}^{(1)} &x_{2}^{(2)} &x_{2}^{(3)} &\cdots &x_{2}^{(m)} \\ \vdots &\vdots &\vdots &\ddots &\vdots \\ x_{n}^{(1)}&x_{n}^{(2)} &x_{n}^{(3)} & \cdots & x_{n}^{(m)} \end{bmatrix}\begin{bmatrix} h_{\theta }(x^{(1)})-y^{(1)}\\ h_{\theta }(x^{(2)})-y^{(2)}\\ h_{\theta }(x^{(3)})-y^{(3)}\\ \vdots\\ h_{\theta }(x^{(m)})-y^{(m)} \end{bmatrix}$

4.4 多元线性回归的矩阵描述

综合4.3中讨论的内容，我们这样定义，并给出多元线性回归的矩阵描述公式

$x^{(i)}=\begin{bmatrix} x_{0}^{(i)} \\ x_{1}^{(i)} \\ x_{2}^{(i)} \\\vdots \\ x_{n} ^{(i)}\end{bmatrix}\in \mathbb{R}^{n+1}$ $\theta =\begin{bmatrix} \theta_{0} \\ \theta_{1} \\ \theta_{2} \\ \vdots \\ \theta_{n} \end{bmatrix}\in \mathbb{R}^{n+1}$

$X=\begin{bmatrix} x_{0}^{(1)} &x_{1}^{(1)} &x_{2}^{(1)} &\cdots &x_{n}^{(1)} \\ x_{0}^{(2)} &x_{1}^{(2)} &x_{2}^{(2)} &\cdots &x_{n}^{(2)} \\ x_{0}^{(3)} &x_{1}^{(3)} &x_{2}^{(3)} &\cdots &x_{n}^{(3)} \\ \vdots &\vdots &\vdots &\ddots &\vdots \\ x_{0}^{(m)}&x_{1}^{(m)} &x_{2}^{(m)} & \cdots & x_{n}^{(m)} \end{bmatrix}= \begin{bmatrix} -x^{(1)T}-\\ -x^{(2)T}-\\ -x^{(3)T}-\\ \vdots\\ -x^{(m)T}- \end{bmatrix}\in \mathbb{R}^{m\times (n+1)}$ $y=\begin{bmatrix} y^{(1)}\\ y^{(2)}\\ y^{(3)}\\ \vdots\\ y^{(m)} \end{bmatrix}\in \mathbb{R}^{m}$

满足 $X\theta=y$

那么梯度下降过程公式为

$\theta $:=$\theta -\alpha \cdot \frac{1}{m}\cdot X^{T}(X\theta -y)$

4.5 平均值归一化 Mean Normalization

Feature Scaling: Get every feature into approximately a range $-1\leqslant x_{j}\leqslant 1$ .

使用梯度下降时，为了加速收敛，应将特征值进行缩放（Feature Scaling）。缩放的具体算法就是Mean Normalization平均值归一化。

Mean Normalization平均值归一化的具体做法是，取得某一维度上特征值的平均值 $u_{j}$ ，最大值 $\max x_{j}$ ，最小值 $\min x_{j}$ 。

进行缩放 $x_{j}=\frac{x_{j}-u_{j}}{\left | \max x_{j}-\min x_{j} \right |}$ ，使缩放后该维度上特征值的平均值接近于0。

注意：

平均值归一化算法只能对维度 $j> 0$ 的特征值进行，决不能对 $x_{0}$ 进行。因为 $x_{0}$ 是人为添加的，都等于1，归一化后 $x_{0}$ 将全部被置为0。
使用了平均值归一化，必须要在这个过程中记录下每个特征的平均值和标准差。在梯度下降得到模型参数以后，给出新的测试样本，那么就要用这个平均值和标准差先对这个测试样本进行平均值归一化，再计算估值。否则，估值是错误的。

4.6 多项式拟合 Polynomial Regression

回归问题也可以采用多项式（开方）来进行拟合。

$h_{\theta}(x)=\theta _{0}+\theta _{1}x+\theta _{2}x^{2}+\theta _{3}x^{3}+\cdots+\theta _{n}x^{n}$

$h_{\theta}(x)=\theta _{0}+\theta _{1}x+\theta _{2}\sqrt x$

4.7 过拟合Overfit与欠拟合Underfit

机器学习问题解决的答案并不是唯一的，我们用一元线性回归可以得到一种估值，也可以用多项式拟合得到另一种估值，也可以用开方的拟合得到另一种估值。不同的估值并没有对错之分，完全取决于我们选择了什么样的模型来解决问题。

对于明显的采用一元线性回归或者开平方拟合就能解决的问题，如果非要使用多项式拟合，在给定的训练集上可能效果很好。但是，随着特征（输入）范围的扩大，拟合效果将可能出现较大偏差，这就是过拟合Overfit。同理，如果我们用一元线性回归（“直线”）去解决一个明显是多项式回归的问题，或者多项式拟合的阶数不够，就会走向另一个极端欠拟合Underfit。

因此，我们应当对训练集的数据进行预处理，剔除明显带有错误或者重大偏差的数据，并小心谨慎的选择解决问题的模型（恰拟合），避免过拟合或欠拟合。

4.8 一般等式、梯度下降和一般等式的比较

根据 $X\theta=y$ ，我们得出一个求参数 $\theta$ 的一般等式。过程并不是严格的数学证明，只是一种演示，不严谨不要喷我。

$X^{T}X\theta=X^{T}y$

$\theta=(X^{T}X)^{-1}X^{T}y$

这样我们不需要经过梯度下降，根据这个公式进行矩阵运算即可求得参数 $\theta$ 。如果使用octave或者matlab等软件，对于求矩阵逆的运算应使用pinv函数，以防止矩阵 $X^{T}X$ 不可逆。

最后对比一下梯度下降和一般等式的优缺点。

梯度下降、一般等式对比
Gradient Decent 梯度下降	Normal Equation 一般等式
Need to choose $\alpha$ 需要选择学习率 $\alpha$	No Need to choose $\alpha$ 不需要选择学习率 $\alpha$
Need many iterations 需要迭代	No need to iterate 不需要迭代
Work well even when n is large 当参数个数n较大时依然性能良好	Need to compute $(X^{T}X)^{-1}$ slow if n is large 需要求矩阵的逆 $(X^{T}X)^{-1}$ 当参数个数n较大时计算缓慢

机器学习01-定义、线性回归、梯度下降

一、定义 What is Machine Learning

二、建模 Model Representation

三、一元线性回归 Linear Regression with One Variable

3.1 一元线性归回的符号约定 Notation

3.2 一元线性回归 Linear Regression with One Variable

3.3 代价函数 Cost Function

3.4 梯度下降概述 Gradient Descent Outline

3.5 梯度下降算法 Gradient Descent Alg

3.5.1 同步更新参数 Simultaneously Update $\theta _{j}$

3.5.2 收敛 Convergence

3.5.3 学习率 $\alpha$ 的取值 evaluate alpha

3.5.4 梯度下降更新参数公式

四、多元线性回归 Multiple Features and Gradient Descent

4.1 多元线性归回的符号约定 Notation

4.2 多元线性回归 Linear Regression with Multiple Variables

4.3 估值、代价函数、梯度下降

4.4 多元线性回归的矩阵描述

4.5 平均值归一化 Mean Normalization

4.6 多项式拟合 Polynomial Regression

4.7 过拟合Overfit与欠拟合Underfit

4.8 一般等式、梯度下降和一般等式的比较

相关文章

ICANN敦促业界使用DNSSEC，应对DNS劫持攻击

一个考查作用域以及闭包的题目

4.65FTP服务4.66测试登录FTP

平台级 SAAS 架构的基础：统一身份管理系统

iOS之runtime详解api(三)

P4722 【模板】最大流

机器学习03-神经网络

数据结构-栈与队列