平衡二叉树的应用举例

news/2024/7/7 18:53:52

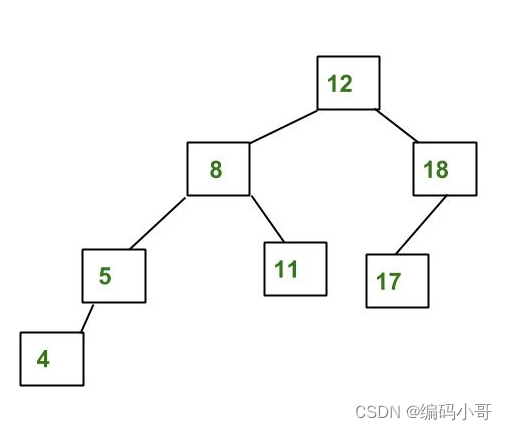
AVL 是一种自平衡二叉搜索树，其中任何节点的左右子树的高度之差不能超过 1。

AVL树的特点：

1、它遵循二叉搜索树的一般属性。

2、树的每个子树都是平衡的，即左右子树的高度之差最多为1。

3、当插入新节点时，树会自我平衡。因此，插入操作非常耗时。

AVL Tree的应用：

1、大多数内存中集和字典都使用 AVL 树进行存储。

2、数据库应用程序（插入和删除不太常见，但需要频繁的数据查找）也经常使用 AVL 树。

3、除了数据库应用程序之外，它还用于其他需要更好搜索的应用程序。

4、有序关联容器（集合、多集、映射和多映射）的大多数 STL 实现都使用红黑树而不是 AVL树。

#include <stdio.h>
#include <stdlib.h>

struct AVLnode
{
    int key;
    struct AVLnode *left;
    struct AVLnode *right;
    int height;
};
typedef struct AVLnode avlNode;

int max(int a, int b) { return (a > b) ? a : b; }

avlNode *newNode(int key)
{
    avlNode *node = (avlNode *)malloc(sizeof(avlNode));

    if (node == NULL)
        printf("!! Out of Space !!\n");
    else
    {
        node->key = key;
        node->left = NULL;
        node->right = NULL;
        node->height = 0;
    }

    return node;
}

int nodeHeight(avlNode *node)
{
    if (node == NULL)
        return -1;
    else
        return (node->height);
}

int heightDiff(avlNode *node)
{
    if (node == NULL)
        return 0;
    else
        return (nodeHeight(node->left) - nodeHeight(node->right));
}

/* 返回左子树中最小值的节点*/
avlNode *minNode(avlNode *node)
{
    avlNode *temp = node;

    while (temp->left != NULL) temp = temp->left;

    return temp;
}

void printAVL(avlNode *node, int level)
{
    int i;
    if (node != NULL)
    {
        printAVL(node->right, level + 1);
        printf("\n\n");

        for (i = 0; i < level; i++) printf("\t");

        printf("%d", node->key);

        printAVL(node->left, level + 1);
    }
}

avlNode *rightRotate(avlNode *z)
{
    avlNode *y = z->left;
    avlNode *T3 = y->right;

    y->right = z;
    z->left = T3;

    z->height = (max(nodeHeight(z->left), nodeHeight(z->right)) + 1);
    y->height = (max(nodeHeight(y->left), nodeHeight(y->right)) + 1);

    return y;
}

avlNode *leftRotate(avlNode *z)
{
    avlNode *y = z->right;
    avlNode *T3 = y->left;

    y->left = z;
    z->right = T3;

    z->height = (max(nodeHeight(z->left), nodeHeight(z->right)) + 1);
    y->height = (max(nodeHeight(y->left), nodeHeight(y->right)) + 1);

    return y;
}

avlNode *LeftRightRotate(avlNode *z)
{
    z->left = leftRotate(z->left);

    return (rightRotate(z));
}

avlNode *RightLeftRotate(avlNode *z)
{
    z->right = rightRotate(z->right);

    return (leftRotate(z));
}

avlNode *insert(avlNode *node, int key)
{
    if (node == NULL)
        return (newNode(key));

    /*二叉搜索树插入*/

    if (key < node->key)
        node->left =
            insert(node->left, key); /*递归插入左子树*/
    else if (key > node->key)
        node->right =
            insert(node->right, key); /*递归插入右子树*/

    /*计算节点高度*/
    node->height = (max(nodeHeight(node->left), nodeHeight(node->right)) + 1);

    /*检查平衡性*/
    int balance = heightDiff(node);

    /*左左*/
    if (balance > 1 && key < (node->left->key))
        return rightRotate(node);

    /*右右*/
    if (balance < -1 && key > (node->right->key))
        return leftRotate(node);

    /*左右*/
    if (balance > 1 && key > (node->left->key))
    {
        node = LeftRightRotate(node);
    }

    /*右左*/
    if (balance < -1 && key < (node->right->key))
    {
        node = RightLeftRotate(node);
    }

    return node;
}

avlNode *delete (avlNode *node, int queryNum)
{
    if (node == NULL)
        return node;

    if (queryNum < node->key)
        node->left =
            delete (node->left, queryNum); /*Recursive deletion in L subtree*/
    else if (queryNum > node->key)
        node->right =
            delete (node->right, queryNum); /*Recursive deletion in R subtree*/
    else
    {
        /*单节点或者没有子节点*/
        if ((node->left == NULL) || (node->right == NULL))
        {
            avlNode *temp = node->left ? node->left : node->right;

            /*没有子节点*/
            if (temp == NULL)
            {
                temp = node;
                node = NULL;
            }
            else /*单节点*/
                *node = *temp;

            free(temp);
        }
        else
        {
            /*两个孩子节点*/

            /*获取右子树最小值的节点*/
            avlNode *temp = minNode(node->right);
            node->key = temp->key; /*拷贝到根节点*/
            node->right =
                delete (node->right,
                        temp->key); /*删除右子树最小值的节点*/
        }
    }

    /*单节点*/
    if (node == NULL)
        return node;

    /*更新高度*/
    node->height = (max(nodeHeight(node->left), nodeHeight(node->right)) + 1);

    int balance = heightDiff(node);

    /*左左*/
    if ((balance > 1) && (heightDiff(node->left) >= 0))
        return rightRotate(node);

    /*左右*/
    if ((balance > 1) && (heightDiff(node->left) < 0))
    {
        node = LeftRightRotate(node);
    }

    /*右右*/
    if ((balance < -1) && (heightDiff(node->right) >= 0))
        return leftRotate(node);

    /*右左*/
    if ((balance < -1) && (heightDiff(node->right) < 0))
    {
        node = RightLeftRotate(node);
    }

    return node;
}

avlNode *findNode(avlNode *node, int queryNum)
{
    if (node != NULL)
    {
        if (queryNum < node->key)
            node = findNode(node->left, queryNum);
        else if (queryNum > node->key)
            node = findNode(node->right, queryNum);
    }

    return node;
}

void printPreOrder(avlNode *node)
{
    if (node == NULL)
        return;

    printf("  %d  ", (node->key));
    printPreOrder(node->left);
    printPreOrder(node->right);
}

void printInOrder(avlNode *node)
{
    if (node == NULL)
        return;
    printInOrder(node->left);
    printf("  %d  ", (node->key));
    printInOrder(node->right);
}

void printPostOrder(avlNode *node)
{
    if (node == NULL)
        return;
    printPostOrder(node->left);
    printPostOrder(node->right);
    printf("  %d  ", (node->key));
}

int main()
{
    int choice;
    int flag = 1;
    int insertNum;
    int queryNum;

    avlNode *root = NULL;
    avlNode *tempNode;

    while (flag == 1)
    {
        printf("\n\nEnter the Step to Run : \n");

        printf("\t1: Insert a node into AVL tree\n");
        printf("\t2: Delete a node in AVL tree\n");
        printf("\t3: Search a node into AVL tree\n");
        printf("\t4: printPreOrder (Ro L R) Tree\n");
        printf("\t5: printInOrder (L Ro R) Tree\n");
        printf("\t6: printPostOrder (L R Ro) Tree\n");
        printf("\t7: printAVL Tree\n");

        printf("\t0: EXIT\n");
        scanf("%d", &choice);

        switch (choice)
        {
        case 0:
        {
            flag = 0;
            printf("\n\t\tExiting, Thank You !!\n");
            break;
        }

        case 1:
        {
            printf("\n\tEnter the Number to insert: ");
            scanf("%d", &insertNum);

            tempNode = findNode(root, insertNum);

            if (tempNode != NULL)
                printf("\n\t %d Already exists in the tree\n", insertNum);
            else
            {
                printf("\n\tPrinting AVL Tree\n");
                printAVL(root, 1);
                printf("\n");

                root = insert(root, insertNum);
                printf("\n\tPrinting AVL Tree\n");
                printAVL(root, 1);
                printf("\n");
            }

            break;
        }

        case 2:
        {
            printf("\n\tEnter the Number to Delete: ");
            scanf("%d", &queryNum);

            tempNode = findNode(root, queryNum);

            if (tempNode == NULL)
                printf("\n\t %d Does not exist in the tree\n", queryNum);
            else
            {
                printf("\n\tPrinting AVL Tree\n");
                printAVL(root, 1);
                printf("\n");
                root = delete (root, queryNum);

                printf("\n\tPrinting AVL Tree\n");
                printAVL(root, 1);
                printf("\n");
            }

            break;
        }

        case 3:
        {
            printf("\n\tEnter the Number to Search: ");
            scanf("%d", &queryNum);

            tempNode = findNode(root, queryNum);

            if (tempNode == NULL)
                printf("\n\t %d : Not Found\n", queryNum);
            else
            {
                printf("\n\t %d : Found at height %d \n", queryNum,
                       tempNode->height);

                printf("\n\tPrinting AVL Tree\n");
                printAVL(root, 1);
                printf("\n");
            }

            break;
        }

        case 4:
        {
            printf("\nPrinting Tree preOrder\n");
            printPreOrder(root);

            break;
        }

        case 5:
        {
            printf("\nPrinting Tree inOrder\n");
            printInOrder(root);

            break;
        }

        case 6:
        {
            printf("\nPrinting Tree PostOrder\n");
            printPostOrder(root);

            break;
        }

        case 7:
        {
            printf("\nPrinting AVL Tree\n");
            printAVL(root, 1);

            break;
        }

        default:
        {
            flag = 0;
            printf("\n\t\tExiting, Thank You !!\n");
            break;
        }
        }
    }

    return 0;
}


http://lihuaxi.xjx100.cn/news/2180994.html

相关文章

LDRA Testbed(TBrun)软件单元测试_操作指南

LDRA Testbed(TBrun)软件单元测试_操作指南

系列文章目录 LDRA Testbed软件静态分析_操作指南 LDRA Testbed软件静态分析_自动提取静态分析数据生成文档 LDRA Testbed软件静态分析_Jenkins持续集成_(1)自动进行静态分析的环境搭建 LDRA Testbed软件静态分析_Jenkins持续集成_(2)配置邮件自动发送静态分析结果 LDRA Testb…
阅读更多...
linux中的“-＞“符号

linux中的“-＞“符号

问&#xff1a; "->“符号在Linux中是什么意思。 例如&#xff1a;当我在一个特定的文件夹中执行ls -l时&#xff0c;我得到了以下结果。 lrwxrwxrwx 1 root root 11 May 16 13:30 nexus3 -> /nexus-data lrwxrwxrwx 1 root root 29 Feb 27 12:23 ojdbc.jar -&g…
阅读更多...
centos时间不对

centos时间不对

检查当前时区是否正确 timedatectl status如果时区不正确&#xff0c;使用以下命令设置正确的时区&#xff08;将Asia/Shanghai替换为您所在的时区&#xff09;&#xff1a; timedatectl set-timezone Asia/Shanghai如果时区正确但时间不准确&#xff0c;使用以下命令同步网络…
阅读更多...
2024年生成式AI使用趋势报告

2024年生成式AI使用趋势报告

生成式AI技术及产品发展概况 人工智能技术奇点降临&#xff0c;搜索成为大模型技术落地的“首站” 过去几十年&#xff0c;人工智能长期鲜有突破性的发展&#xff0c;直至2022年AI大模型技术奇点的出现&#xff0c;使得AI能力发生了颠覆性的变化&#xff0c;人工智能受到了前…
阅读更多...
前端传String字符串 后端使用enun枚举类出现错误

前端传String字符串 后端使用enun枚举类出现错误

情况 前端 String 后端 enum 前端 后端 报错 2024-05-31T21:47:40.61808:00 WARN 21360 --- [nio-8080-exec-6] .w.s.m.s.DefaultHandlerExceptionResolver : Resolved [org.springframework.web.method.annotation.MethodArgumentTypeMismatchException: Failed to con…
阅读更多...
windows安装nodeJs,以及常用操作

windows安装nodeJs,以及常用操作

1. 官网(Node.js — Run JavaScript Everywhere (nodejs.org))下载想要安装的node版本 的安装包完成安装 2.环境变量设置&#xff1a; 系统变量&#xff1a; Path新增&#xff1a;D:\Program Files\nodejs (node安装目录) 3.设置淘宝源&#xff1a; npm config set registr…
阅读更多...
天文学专业大学院校排名（2024最新排行榜）

天文学专业大学院校排名（2024最新排行榜）

序号 学校代码 学校名称 学科名称 评估结果 1 10284 南京大学 天文学 A 2 10358 中国科学技术大学 天文学 A 3 10001 北京大学 天文学 B- 4 10248 上海交通大学 天文学 C 5 10027 北京师范大学 天文学 C- 天文学专业排名前5名的大学有&#xff1…
阅读更多...
数据结构基础篇(5)

数据结构基础篇(5)

二十一.栈和队列的定义和特点 栈 栈的定义 栈是一个特殊的线性表&#xff0c;是限定仅在一段(通常是表尾)进行插入和删除操作的线性表又叫后进后出段的线性表&#xff0c;LIFO结构栈的概念 栈是仅在表尾进行插入&#xff0c;删除操作的线性表表尾叫栈顶Top&#xff1b;表头叫栈…
阅读更多...
最新文章

Copyright @ 2022~2023