一、说明
数学家总是痴迷于根据乍一看似乎完全无关的事实/观察来形成概括。为什么?原因很简单,如果我们知道相同的骨架是不同数学结构的基础,那么我们就可以只详细研究一种结构,并确信其他结构也会得到类似的结果。这不是节省了很多时间吗!
在本文中,我们将探讨这样一个结果——拉格朗日定理。该定理是数学最不可或缺的分支之一群论的初步结果。该定理最初由拉格朗日于 1770 年以非群论术语陈述。然而,30 年后,彼得罗·阿巴蒂 (Pietro Abbati) 提供了第一个完整的证据。
本文的结构如下:
- 定义组。
- 定义子组和余集。
- 拉格朗日定理及其证明。
- 闭幕词。
所有这些都将通过贯穿整篇文章的常见示例来说明。所以,让我们开始吧!
二、引出群概念
考虑一个集合 G,以及一个二进制运算 – *。现在,我们说 (G, *) 如果满足以下所有条件,则形成一个组——
- 该操作在 G 中关闭。也就是说,对于属于 G 的任意两个元素 a 和 b,a * b 也属于 G。
- 该操作是关联的。也就是说,对于属于 G 的任意三个元素 a、b 和 c,我们有:a * (b * c) = (a * b) * c。
- 该操作在 G 中具有标识元素。该元素通常用 e(来自德语中的统一词 Einheit)表示,并且具有以下属性:e * a = a * e = a,对于属于 G 的每个元素 a。
- 对于 G 的每个元素 a,都存在一个属于 G 的元素 a',因此,我们有:a * a' = a' * a = e。
请注意,运算 * 有时表示为“.”,有时甚至根本没有记下。因此,以下三个表达式代表同一件事——
- a *b
- a.b
- ab
现在,让我们快速熟悉一个我们将在整个文章过程中使用的示例!
2.1 加法模数 6
如果您不知道模的含义,您会惊讶地发现您已经在一天中多次使用该操作!每当你看时钟时,你都在使用加法模 12(或 24)。例如,您如何确定上午 10 点之后的 5 小时是下午 3 点,而不是凌晨 15 点?您可以通过四舍五入大约 12 来做到这一点。也就是说,将 5 加到 10 得到 15,然后查看它从 12 中得到的余数。
这种执行加法然后从固定数中取余数的操作称为模块化加法。固定数字用作上限柱,数字盘回起点。在符号中,我们将上面的例子表示为——
(10 + 5) 模组 12 = 3
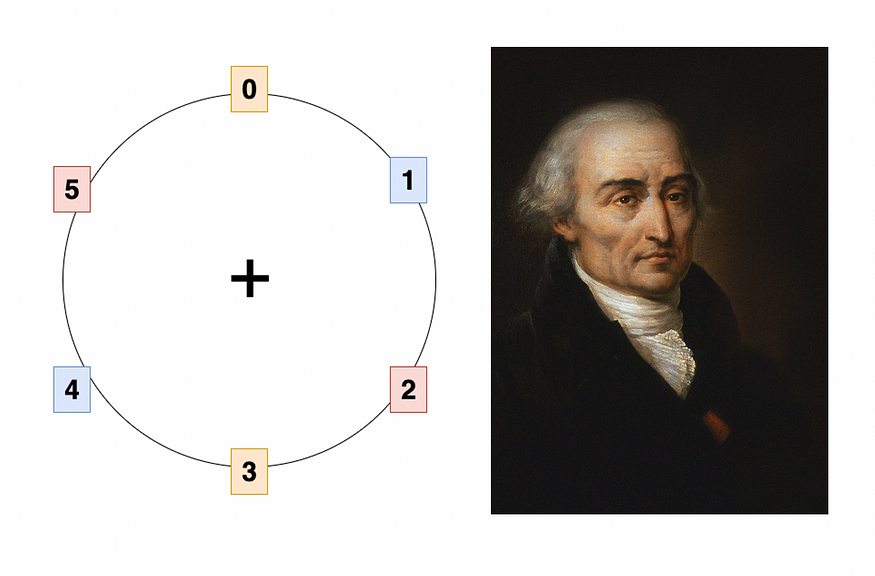
现在,考虑集合 S = {0, 1, 2, 3, 4, 5} 以及加法模 6 的运算。那是–
a * b = (a + b) mod 6
例如,5 * 3 = (5 + 3) mod 6 = 8 mod 6 = 2
在表格形式中,这可以表示为——
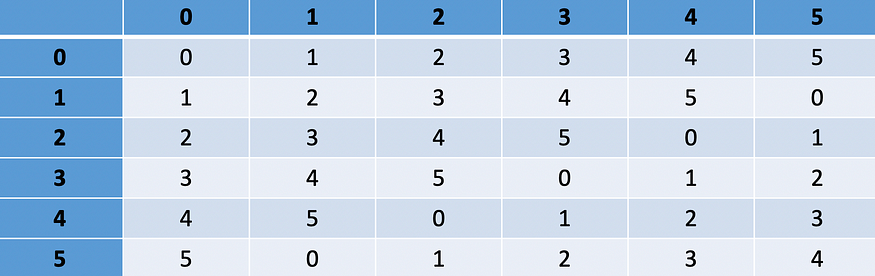
(a + b) 模组 6.在这里,a 是行元素,而 b 是列元素。
读者可以很容易地验证上述结构是否满足一个组的所有标准,因此确实是一个!恒等式为 0,逆数可从上表轻松获得。
此外,它有助于考虑循环形式的模块化添加——
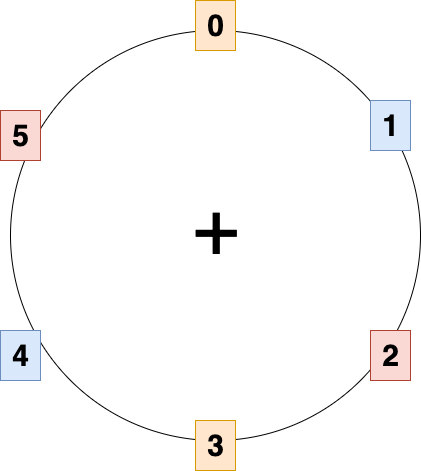
参考上图,我们需要做的就是将两个数字 a 和 b 相加——我们从 a 开始,顺时针移动 b 单位,我们降落的地方是 (a + b) mod 6!例如,如果我们从 2 开始并顺时针方向移动 5 个单位,我们将以 1 结束。这是因为 (2 + 5) mod 6 = 1。
2.2 子群和子集
顾名思义,子组是组的子集,它本身就是一个组(当然,对于相同的操作)。继续上面的例子,我们看到我们组有四个子组——
- H_1 = {0}
- H_2 = {0, 3}
- H_3 = {0, 2, 4}
- H_4 = {0, 1, 2, 3, 4, 5} (即 G 本身)
在这里,我们只对适当的子组(不等于父组的子组)感兴趣,因此我们可以忽略H_4。此外,H_1是微不足道的子组。这两个子组(组本身和琐碎子组)将始终存在于一个组中。H_2 和 H_3 是我们感兴趣的非平凡的、适当的子组。
在表格符号中,我们有——
H_2 = {0, 3}

H_3 = {0, 2, 4}

请注意,每个子组的标识保持不变!
在循环表示法中,这两个子组可以可视化为——
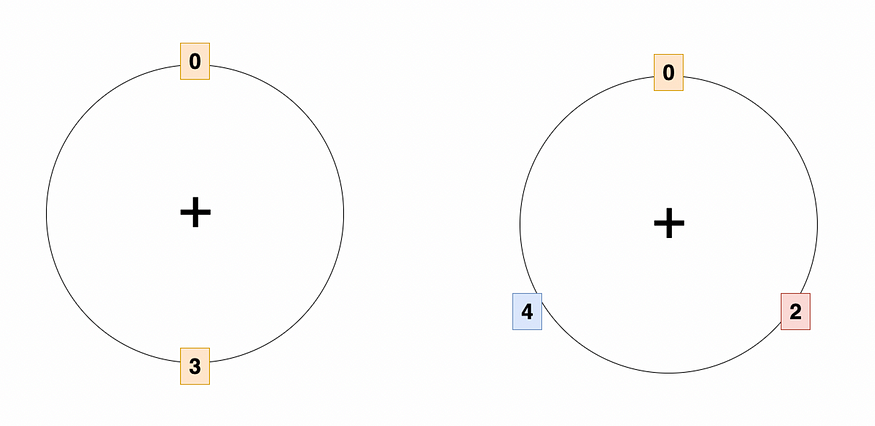
两个非平凡的正确子组:{0, 3} 和 {0, 2, 4}。
coset的概念与一个子群相关联。为了探索它,让我们继续使用示例中的特定子组:
H_2 = {0, 3}。
为方便起见,让我们采取——
G = {0, 1, 2, 3, 4, 5}
H = {0, 3}
现在,对于属于 G 的任何元素 a,我们将相应的 coset aH 定义为 –
aH = {通过对 H 的元素进行操作 a 获得的所有元素的集合}
示例:对于我们的子组 {0, 3} —
- 对应于 4 的 coset 将是 – {(4 + 0) mod 6, (4 + 3) mod 6} = {4, 1}
- 对应于 5 的 coset 是 — {(5 + 0) mod 6, (5 + 3) mod 6} = {5, 2}
三、拉格朗日定理
进入本文的正题,我们现在提出并证明一个基本的群论结果,这个结果早于分支本身(当然,这意味着它最初是用非群论术语陈述的)。
对于任何有限群 G,G 的任何子群中的元素数必须是 G 中元素数的因数。
继续我们的例子,我们有——
- G = {0, 1, 2, 3, 4, 5}
- H_1 = {0}
- H_2 = {0, 3}
- H_3 = {0, 2, 4}
- H_4 = {0, 1, 2, 3, 4, 5}
请注意,组的大小是 6,子组的大小是 1、2、3 和 6 – 所有因子都是 6!
请注意,拉格朗日定理限制了子群的可能大小。大小为 6 的组不能有大小为 4 的子组,因为 4 不会除以 6。同样,大小为 8 的组只能具有大小为 1、2、4 和 8 的子组。
现在,让我们来证明这个定理吧!但要做到这一点,我们首先需要围绕 coset 建立更多的结果。
3.1 结果 1
a 属于 coset aH。
证据很简单。每个子群 H 都包含恒等式 e(可以很容易地证明)。因此,相应的 coset 将包含元素 a * e = a。
示例 — 继续 G 和 H = {0, 3},对应于 4 的 coset 是 {4, 1},其中包含 4。
3.2 结果 2
aH 的大小与 H 相同。
显然,aH 的大小不能大于 H。因此,如果我们能证明对于属于 H 的任何两个不同元素 x、y、ax ≠ ay,那么我们就完成了。这意味着 aH 没有重复,因此大小与 H 相等。
这可以通过使用团体取消属性来轻松证明。因为,如果 ax = ay,那么我们有——
a'ax = a'ay,这给出了 x = y。
示例 — 对于 H = {0, 3},我们有 —
- Coset 对应于 4 = {4, 1},其大小等于 H。
- 类似地,对于对应于 5 的 coset({5, 2} 的大小等于 H 的大小)。
3.3 结果 3
与两种不同元素 aH 和 bH 相关的 Coset 要么是不相交的(没有共同的元素),要么彼此完全相等!
这是一个相当了不起的结果!让我们首先借助示例来理解它。
G = {0, 1, 2, 3, 4, 5}, H = {0, 3}
对应于 H 的 Coset 是 —
- 0H = {0, 3}
- 1H = {1, 4}
- 2H = {2, 5}
- 3H = {3, 0}
- 4H = {4, 1}
- 5H = {5, 2}
请注意,没有两个具有部分相交的 coset——每对要么不相交,要么完全相同!
现在,让我们去证明这一点。
设 a 和 b 是 G 的两个不同元素。然后,可能有两种情况——
- aH 和 bH 不相交。在这种情况下,没有什么可证明的。
- aH 和 bH 至少有一个共同点。在这种情况下,我们需要证明它们实际上是相同的,也就是说,具有所有共同点!
为了证明上述情况,设 z 是 aH 和 bH 之间的公共元素。然后,我们必须让 x、y 属于 H,使得 ax = z = by (1)。
现在,让 p 是属于 aH 的任何元素。那么一定有一些属于 H 的 w,这样——
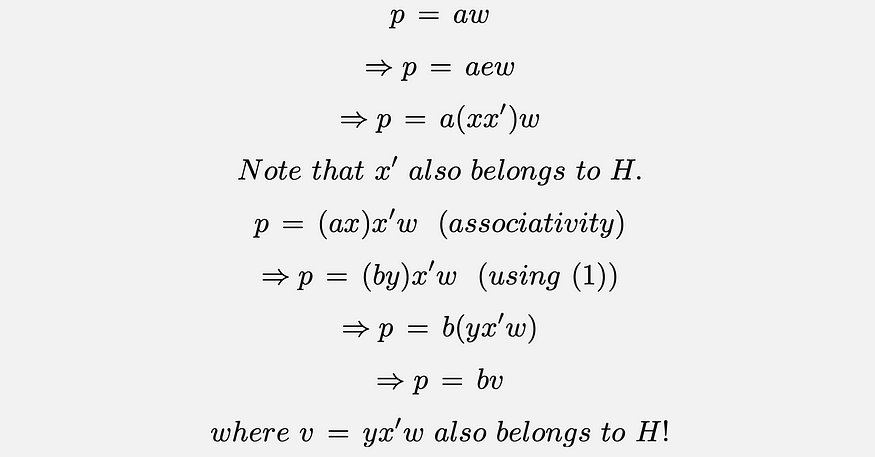
因此 p 属于 bH!因此,任何属于 aH 的元素都属于 bH。按照与上述类似的思路,我们可以很容易地证明 bH 的每个元素也属于 aH。结合在一起,我们看到 aH 和 bH 是一回事!因此证明。
最后,我们可以证明拉格朗日定理了!
3.4 拉格朗日定理的证明
考虑 coset aH, bH, cH, ...,其中 a, b, c ...是 G 的元素。现在,由于 a 属于 aH(结果 1),b 属于 bH,c 属于 cH ...,因此,如果我们取所有这些 coset 的并集,那么它将包含 G 的所有元素。那是–
G = aH ∪ bH ∪ cH ∪ ...
继续我们的例子——
G = {0, 1, 2, 3, 4, 5}, H = {0, 3}
使用对应于 {0, 3} 的 coset,我们有 —
G = {0, 3} ∪ {1, 4} ∪ {2, 5} ∪ {3, 0} ∪ {4, 1} ∪ {5, 2}
现在,从上面的结果 3 中,我们知道给定任何两个 coset,它们只能以以下两种方式之一相关——
- 它们要么彼此相同,要么
- 它们将完全脱节。
这使我们能够进行简化。由于在并集时多次出现同一集合是没有意义的,因此我们只取一个并留下其余的。也就是说,如果 pH = qH = rH(比如说),那么我们只需在上面的等式中只取其中一个,省略其他的。
为了方便起见,让我们假设 a、b、c、...,现在已经取得 aH、bH、cH、...,都是成对不相交的。换句话说,我们现在已经从上面的表达式中删除了重复项。
G = aH ∪ bH ∪ cH ∪...,(其中 aH, bH, cH ,...都是平分秋色的不相交)
在我们的示例中,我们看到以下三个 coset 各出现两次——
- {0, 3}
- {1, 4}
- {2, 5}
因此,只计算每次出现一次,我们就有——
G = {0, 3} ∪ {1, 4} ∪ {2, 5}
现在,双方的元素数量应该相等。那就是——
尺寸(G) = 尺寸 (aH ∪ bH ∪ cH ∪ ...)
由于右手边的所有集合都是成对不相交的,我们有——
尺寸(G) = 尺寸 (aH ∪ bH ∪ cH ∪ ...),简化为
尺寸(G) = 尺寸(aH) + 尺寸(bH) + 尺寸(cH) + ...
但是,请注意,每个 coset 的大小等于 H 的大小(结果 2)!因此,我们有——
尺寸(G) = 尺寸(H) + 尺寸(H) + 尺寸(H) + ...,或
尺寸(G) = k.尺寸(H)
其中 k 是上式中存在的不同 coset 的数量。
我们有了它!通俗地说,上面的等式说 H 的元素数是 G 的元素数的一个因数。这就是我们要证明的!
最后,以我们的例子来结束——

四、后记
上述定理完美地结合了数学直觉和严谨性。虽然这个定理本身是凭直觉出现在我们的脑海中的,但证明是非常严谨的,在此过程中引入了 coset 的新想法。
在他杰出的著作《数学家的道歉》中,GH Hardy描述了两个参数,他认为这两个参数将伟大的证明/结果与普通的证明/结果区分开来——
- 一般性:证明的一般性。涉及许多特殊起始条件的证明,或诸如if,else,but,...在这个指标下表现不佳。
- 深度:对于特定数学分支而言,证明的初级或基本程度。
拉格朗日定理在上述两个标准中得分很高。